Final Project
Final Project: Basic Proposal for “Adaptive Monocular 3D Focus”
Goal:
The main goal of this project was to create an inexpensive method to generate a “3D photograph” (to be more precise, to create an image with 3D structure) with readily available hardware.
Completed: December 2005
Motivation:
My main motivation is to generate a new image where we can understand a new perspective of it: how much space it occupies in a 3D environment. After completing assignment #2, and viewing [Gasperini03]’s images, I was intrigued by the possibility of using one camera to generate a 3D image. Generally, the most popular ways of generating 3D images involve specific hardware, like stereo cameras [Gasperini03], or it would be necessary to have two or more cameras at different perspectives in order to generate a 3D image. However, such a setup is not practical for most of us who have just one digital camera. I thought that there should be another method, a less cumbersome and more readily available technique that could be used to generate a 3D image.
Approach:
The hardware required consists of the Canon A610 Powershot, and a tripod. The software was designed as follows. First, we needed some parameter to determine the pixels in most focused, as described in [Nayar94]. However, instead of using the technique specified in [Nayar94], I determined the pixel in most focused by determining the variance along a 3×3 area of a specific pixel for each image, and thus determined that the pixel with highest variance is the sharpest in-focus pixel. There are certain assumptions and constraints that need to be made for this technique to work. First, we need a highly textured image, an image with reflectance or other parameters that allow for it to have distinguishable variance when it is in focus and when it’s not. Second, the images have to be taken by varying the depth of field of the camera at a constant interval. As expected, the smaller the interval, the more detail and depth the 3D image will have. This differs greatly from [Nayar94] in that it is not necessary for the user to know the measurements of the camera lens, or the distance between the lens and scene. Also, one is able to capture larger objects, such as LEGO’s, rather than microscopic objects.
This technique was identical to the one described in Assignment 2. By directly using this technique, we can acquire the depth of an image by simply reading its location along the array of images. Yet, in order to smooth out the noise generated by this initial method (see Assignment 2 for more details), we applied both a median filter and a most-common value filter (where we keep the most common value from an 3×3 array of pixels as the value of our desired pixel).
Our second was approach was to implement the d-bar function described by [Nayar94]. According to the paper, we can assume that our measured most focused pixel would be close to the theoretical value for the pixel in most focus. Therefore, by using a Gaussian model[1], we can then determine the depth at which it is theoretically in most focused by comparing it with pixels from images above and below the image with the most in-focus pixel. The original equation described is here. In our version, d-bar is still the expected depth of the image, Dm represents the depth measured (where m indicates the location of the highest in-focus pixel). There were some assumptions made here as well, for example pixels with depth= 1 or depth = size of the array were kept the same, and whenever the variance was 0 we set its logarithm equal to one.
I also attempted to implement the graphs cuts specified by [Agarwala04] in order to allow the user to select which parts of the image to render in 3D, similar to allowing the users specify certain parameters from which to generate a 3D structure described in [Zhangy01].
Results:
There were two sets of images used. The first was the same one as used in Assignment #2, while the second one was one that I took. The taken dataset was composed of 20 images, each with a constant varying depth of field. The algorithm, after vectorizing certain function, generated the depth map in 6 minutes on a Athlon 64-Bit 2.3 GHz processor with 1GB Ram. On a 1000MHz Pentium III laptop, it took 40 minutes. This measurement is constant for images taken around 200 – 400 x 300 – 500 resolution.
From Coarse Method:

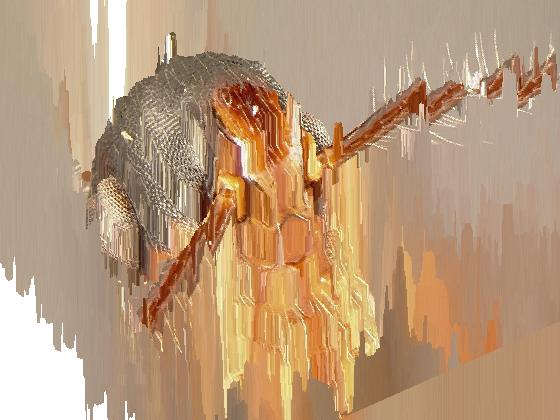
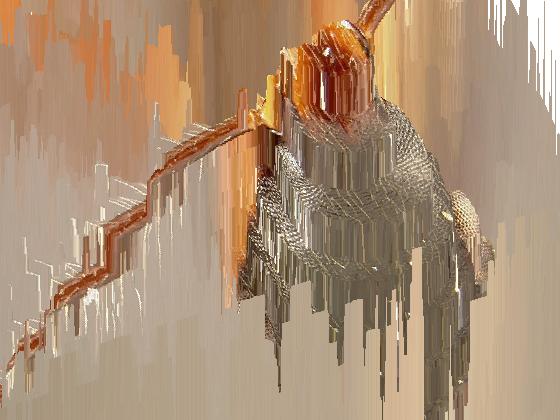

As you can see, the results were a success. As expected, the depth transition of the images is not smooth.
Results from Gaussian Model:

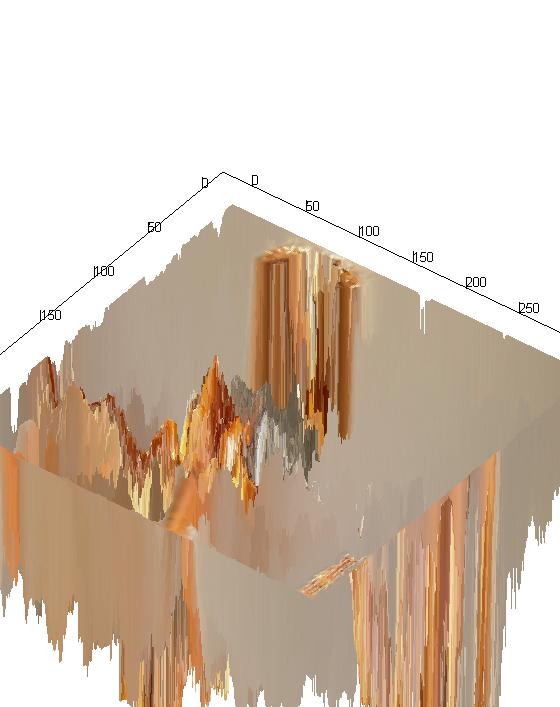
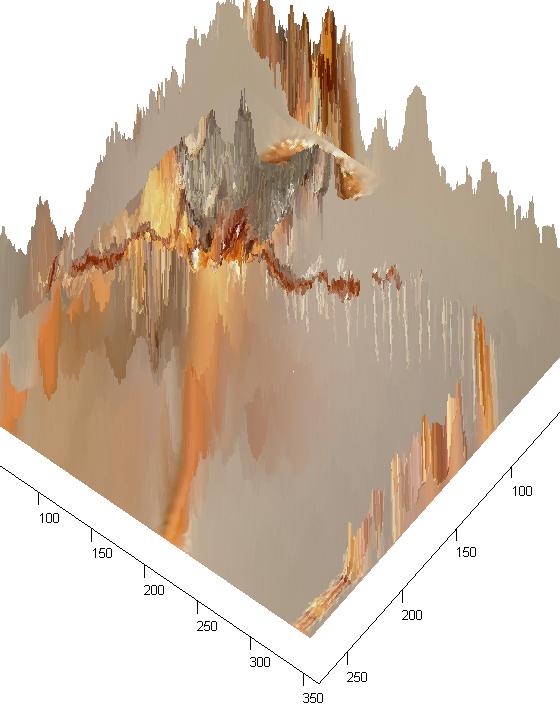
The quality of these images was downgraded so as to be able to render the 3D image quickly on the aforementioned laptop. Nevertheless, they provide an interesting perspective of the scene captured.
When I attempted to implement a graph cut as a way of allowing the user to select which area to render in 3D, I used a recursive algorithm. Alas, it was not successful so I decided to have the user draw a rectangle to select the area desired. Here are the results of that:



Note: The last two images show the actual depth of the images, where the tallest columns represent the deepest location of the pixels.
Results with my Dataset



Note: The last image is shown with the depth parameters inverted
Selected Area


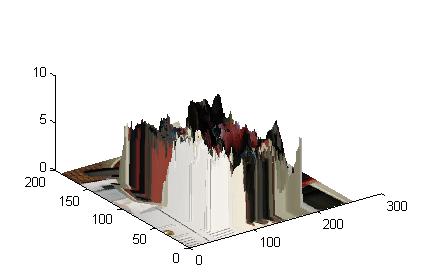
Note: The last image is shown with the depth parameters inverted
Lessons Learned: As expected, acquiring a 3D structure from a single camera with varying depth of focus is difficult. However, I hope to have shown that, through the procedures specified, there are inexpensive and readily available methods to generate 3D images that allow to user to explore new dimensions of their images. Though the algorithms are not perfect, and they could be improved in speed, as well as fixing some of the bugs inherent in them, I consider this project to be a success. I accomplished my goals of learning new, less traditional ways of generating 3D structures that are still coherent to the human eye.
References:
[Zhangy01] L. Zhangy, et. al “Single View Modeling of Free-Form Scenes”
[Nayar94] S.K. Nayar and Y. Nakagawa “Shape from Focus”
[Subbarao95] M. Subbarao, and T. Choi “Accurate Recovery of Three-Dimensional Shape from Image Focus”
[Agarwala04] A. Agarwala, et. al “Interactive Digital Photomontage”
[Gasperini03] J. Gasperini “Time for Space Wiggle”
Files
finalProject.zip : contains all datasets and matlab functions used.

